
眾所周知,統(tǒng)計學(xué)是數(shù)據(jù)分析的基石。學(xué)了統(tǒng)計學(xué),你會發(fā)現(xiàn)很多時候的分析并不那么準(zhǔn)確,比如很多人都喜歡用平均數(shù)去分析一個事物的結(jié)果,但是這往往是粗糙的。而統(tǒng)計學(xué)可以幫助我們以更科學(xué)的角度看待數(shù)據(jù),逐步接近這個數(shù)據(jù)背后的“真相”。 大部分的數(shù)據(jù)分析,都會用到統(tǒng)計方面的知識,可以重點學(xué)習(xí):閱讀路線:
概率介紹
離散型概率分布和連續(xù)型概率分布
抽樣和抽樣分布
區(qū)間估計
假設(shè)檢驗
一. 概率介紹
概率是指的對于某一個特定事件的可能性的數(shù)值度量,且在0-1之間。我們拋一枚硬幣,它有正面朝上和反面朝上兩種結(jié)果,通常用樣本空間S表示,S={正面,反面},而正面朝上這一特定的試驗結(jié)果叫樣本點。對于樣本空間少的試驗,我們極易觀察出他們樣本空間的大小,而對于較復(fù)雜的試驗,我們就需要學(xué)習(xí)些計數(shù)法則了。
(1)多步驟試驗的計數(shù)法則
如果一個試驗可以分為循序的k個步驟,在第1步中有N1種試驗結(jié)果,在第2步中有N2種試驗結(jié)果...以此類推。那么所有的試驗結(jié)果的總數(shù)為N1*N2*N3...*Nk。
舉例:拋兩枚硬幣,第一枚有正反兩種結(jié)果,第二枚有正反兩種結(jié)果。所以試驗結(jié)果的總數(shù)是 2X2=4。
(2)組合計數(shù)法則
從N項中任取n項的組合數(shù):

N和n的上下位置與我們平常見的是相反的。因為我們這里是以歐美規(guī)范為主。
舉例子:從5個彩色球中,選出2個彩球,有多少種選法?

(3)排列計數(shù)法則
從N項中任取n項的排列數(shù)

舉例子:從5個彩色球中,選出2個彩球,有多少種排列方法?
代入得出答案是20種。
(1)事件
其實事件為樣本空間的一個子集,通常,如果能確定一個試驗的所有樣本點并且能夠知曉每個樣本點的概率,那么我們就能求出事件的概率。
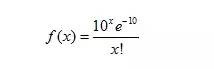
(2)概率的基本性質(zhì)
事件A的補:指的是所有不包含在事件A中的樣本點所以事件A發(fā)生的
概率 P(A)=1-P(A-)。
事件的組合:并和交

兩個圓形區(qū)域所在的部分就是事件A和B的并,其中重疊的部分說明有一些樣本點即屬于A又屬于B,它可以稱之為交。
得出加法公式為:
P(A∪B) = P(A)+P(B) – P(A∩B)。P(A∪B) 是兩個圓形面積,P(A)是藍色圓面積,P(B)是橙色圓面積,當(dāng)兩者相加時,會多出一塊重疊區(qū)域,于是減去P(A∩B)進行修正,得出正確的結(jié)果。
如果某個事件A發(fā)生的可能性受到另外一個事件B的影響,此時A發(fā)生的可能性叫做條件概率,記作P(A|B)。表明我們是在B條件已經(jīng)發(fā)生的條件下考慮A發(fā)生的可能性,統(tǒng)計學(xué)中稱為給定條件B下事件A的概率。

進而又得出了乘法公式:

(3)貝葉斯定理
簡單的來講,貝葉斯定理其實就是,我們先假設(shè)一個事件發(fā)生的概率,然后又找到一個信息,最后得出在這個信息下這一事件發(fā)生的概率。
舉一個我們生活中的例子,當(dāng)我們和一個被懷疑做壞事的人聊天時,我們首先假設(shè)他做壞事的概率為a,然后我們根據(jù)和他交談的信息,得出對他新的認識,重新判斷他做壞事的概率b。
貝葉斯就是闡述了這么一個事實:
新信息出現(xiàn)后B的概率=B的概率 X 新信息帶來的調(diào)整
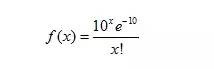
如果當(dāng)直接計算P(A)較為困難時,而P(Bj),P(A|Bj) (j=1,2,...)的計算較為簡單時,可以利用全概率公式計算P(A)。
思想就是,將事件A分解成幾個小事件,通過求小事件的概率,然后相加從而求得事件A的概率,而將事件A進行分割的時候,不是直接對A進行分割,而是先找到樣本空間Ω的一個個劃分B1,B2,...Bn,這樣事件A就被事件AB1,AB2,...ABn分解成了n部分,即A=AB1+AB2+...+ABn, 每一Bj發(fā)生都可能導(dǎo)致A發(fā)生相應(yīng)的概率是P(A|Bj),由加法公式得
P(A)=P(AB1)+P(AB2)+....+P(ABn)
=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(PBn)
所以調(diào)整后的貝葉斯公式為:
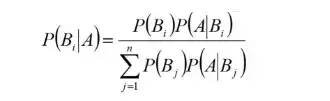
二. 離散型概率分布和連續(xù)型概率分布
概率中通常將試驗的結(jié)果稱為隨機變量。隨機變量將每一個可能出現(xiàn)的試驗結(jié)果賦予了一個數(shù)值,包含離散型隨機變量和連續(xù)型隨機變量。
既然隨機變量可以取不同的值,統(tǒng)計學(xué)家就用概率分布描述隨機變量取不同值的概率。相對應(yīng)的,有離散型概率分布和連續(xù)型概率分布。
數(shù)學(xué)期望是對隨機變量中心位置的一種度量。是試驗中每次可能結(jié)果乘以其結(jié)果的概率的總和。簡單說,它是概率中的平均值。

方差隨機變量的變異性或者是分散程度的度量。

其中的u就是E(x)。
(1)二項概率分布
二項分布是一種離散型的概率分布。故明思義,二項代表它有兩種可能的結(jié)果,把一種稱為成功,另外一種稱為失敗。
除了結(jié)果的規(guī)定,它還需要滿足其他性質(zhì):每次試驗成功的概率均是相同的,記錄為p;失敗的概率也相同,為1-p。每次試驗必須相互獨立,該試驗也叫做伯努利試驗,重復(fù)n次即二項概率。擲硬幣就是一個典型的二項分布。當(dāng)我們要計算拋硬幣n次,恰巧有x次正面朝上的概率,可以使用二項分布的公式:

且二項概率的數(shù)學(xué)期望為E(x) = np,方差Var(x) = np(1-p)。
(2)泊松概率分布
泊松概率是另外一個常用的離散型隨機變量,它主要用于估計某事件在特定時間或空間中發(fā)生的次數(shù)。比如一天內(nèi)中獎的個數(shù),一個月內(nèi)某機器損壞的次數(shù)等。
泊松概率的成立條件是在任意兩個長度相等的區(qū)間中,時間發(fā)生的概率是相同的,并且事件是否發(fā)生都是相互獨立的。
泊松概率既然表示事件在一個區(qū)間發(fā)生的次數(shù),這里的次數(shù)就不會有上限,x取值可以無限大,只是可能性無限接近0,f(x)的最終值很小。
x代表發(fā)生x次,u代表發(fā)生次數(shù)的數(shù)學(xué)期望,概率函數(shù)為:
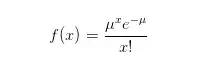
其中泊松概率分布的數(shù)學(xué)期望和方差是相等的。
上述分布都是離散概率分布,當(dāng)隨機變量是連續(xù)型時,情況就完全不一樣了。因為離散概率的本質(zhì)是求x取某個特定值的概率,而連續(xù)隨機變量不行,它的取值是可以無限分割的,它取某個值時概率近似于0。連續(xù)變量是隨機變量在某個區(qū)間內(nèi)取值的概率,此時的概率函數(shù)叫做概率密度函數(shù)。
(1)均勻概率分布
隨機變量x在任意兩個子區(qū)間的概率是相同的。
均勻概率密度函數(shù)
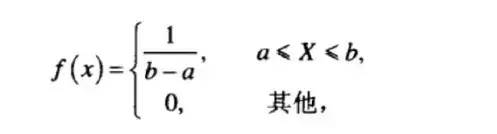
數(shù)學(xué)期望

方差

(2)正態(tài)概率分布
正態(tài)概率分布是連續(xù)型隨機變量中最重要的分布。世界上絕大部分的分布都屬于正態(tài)分布,人的身高體重、考試成績、降雨量等都近似服從。
正態(tài)分布如同一條鐘形曲線。中間高,兩邊低,左右對稱。想象身高體重、考試成績,是否都呈現(xiàn)這一類分布態(tài)勢:大部分?jǐn)?shù)據(jù)集中在某處,小部分往兩端傾斜。

正態(tài)概率密度函數(shù)為:

u代表均值,σ代表標(biāo)準(zhǔn)差,兩者不同的取值將會造成不同形狀的正態(tài)分布。均值表示正態(tài)分布的左右偏移,標(biāo)準(zhǔn)差決定曲線的寬度和平坦,標(biāo)準(zhǔn)差越大曲線越平坦。
一個正態(tài)分布的經(jīng)驗法則:
正態(tài)隨機變量有69.3%的值在均值加減一個標(biāo)準(zhǔn)差的范圍內(nèi),95.4%的值在兩個標(biāo)準(zhǔn)差內(nèi),99.7%的值在三個標(biāo)準(zhǔn)差內(nèi)。

均值u=0,標(biāo)準(zhǔn)差σ=1的正態(tài)分布叫做標(biāo)準(zhǔn)正態(tài)分布。它的隨機變量用z表示,將均值和標(biāo)準(zhǔn)差代入正態(tài)概率密度函數(shù),得到一個簡化的公式:

為了計算概率需要學(xué)習(xí)一個新的函數(shù)叫累計分布函數(shù),它是概率密度函數(shù)的積分。用P(X<=x)表示隨機變量小于或者等于某個數(shù)值的概率,F(xiàn)(x) = P(X<=x)。
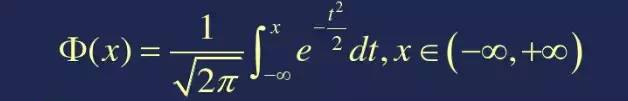
曲線f(x)就是概率密度函數(shù),曲線與X軸相交的陰影面積就是累計分布函數(shù)。
標(biāo)準(zhǔn)正態(tài)分布的分布函數(shù):
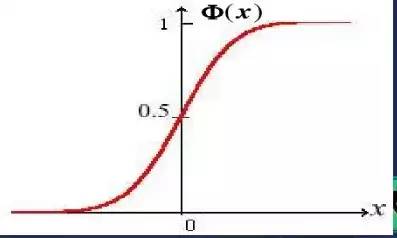
圖像如下:

計算三種類型的概率(這里需要說明一點,只有標(biāo)準(zhǔn)正態(tài)分布時,隨機變量才用z表示)。
1. z小于或者等于某個給定值的概率,直接帶入分布函數(shù)得出
如:p(z<=1)=φ(1)=0.8413 (1值左邊標(biāo)準(zhǔn)正態(tài)曲線下的面積)。
2. z在給定的兩個值之間的概率
如:P(-1<=z<=1.25) = P(z<=1.25) – P(z<=-1) =φ(1.25)-φ(1) =0.735。
3. z大于或者等于某個給定值的概率
如:P(z>1) = 1-P(z<=1) =1-φ(1)= 0.1586。
標(biāo)準(zhǔn)正態(tài)分布與一般的正態(tài)分布的關(guān)系:
任何一個一般的正態(tài)分布都可以通過線性變換轉(zhuǎn)化為標(biāo)準(zhǔn)正態(tài)分布。它依據(jù)的定理如下:

下面做一道題目練習(xí)吧!
現(xiàn)在有一個u=10和σ=2的正態(tài)隨機變量,求x在10與14之間的概率是多少?
當(dāng)x=10時,z=(10-10)/2=2。當(dāng)x=14時,z=(14-10)/2=2。于是x在10和14之間的概率等價于標(biāo)準(zhǔn)正態(tài)分布中0和2之間的概率。計算P(0<=z<=2) =P(z<=2) – P(z<=0) =0.4772。
(3)指數(shù)概率分布
指數(shù)概率密度函數(shù)

其中,x>=0,u為均值,e=2.71828;
計算概率
指數(shù)隨機變量取小于或者等于某一特定值X0的概率
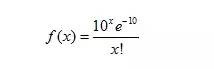
且指數(shù)概率分布的期望=標(biāo)準(zhǔn)差。
(4)指數(shù)分布vs泊松分布
泊松分布:1.是離散型概率分布 2.描述每一區(qū)間中事件發(fā)生的次數(shù)。
指數(shù)分布:1.是連續(xù)型概率分布 2.描述事件發(fā)生的時間間隔的長度。
為了說明問題,簡單舉兩個小例子:
①20分鐘內(nèi)購買肯德基早餐的人數(shù)的均值是10人,那么如果求每20分鐘有x人購買的概率,就應(yīng)該用泊松概率函數(shù):

②20分鐘內(nèi)購買肯德基早餐的人數(shù)的均值是10人,那么如果求每20分鐘這一區(qū)間內(nèi),兩位顧客購買的時間間隔為小于x0的概率,就應(yīng)該用指數(shù)概率函數(shù)。
購買的間隔均值為u=10/20=0.5
把u帶入下面的公式

三. 抽樣和抽樣分布
首先不管是從有限總體中抽樣還是從無限總體中抽樣都應(yīng)該滿足抽樣的隨機性。
我們抽樣得出樣本統(tǒng)計量就是為了估計總體的參數(shù)。
樣本均值(x拔)是總體均值的u的點估計:

樣本標(biāo)準(zhǔn)差s是總體的標(biāo)準(zhǔn)差σ的點估計:

樣本比率(p拔)是總體比率的p的點估計:

其實當(dāng)我們抽樣的時候,我們抽取的每個樣本的均值、方差、比率,可能都是不同的,如果我們把抽取一個簡單的隨機樣本看作一次試驗,那么(x拔)就有期望、方差、標(biāo)準(zhǔn)差和概率分布了((x拔)的概率分布也就是(x拔)的抽樣分布)。
(1)樣本均值的抽樣分布
(x拔)的抽樣:樣本均值(x拔)的所有可能值的概率分布。
(x拔)的數(shù)學(xué)期望:

其中u是總體的期望。
(x拔)的標(biāo)準(zhǔn)差
當(dāng)樣本容量占總體5%以上時,有求樣本標(biāo)準(zhǔn)差公式如下:

當(dāng)樣本容量占總體5%以下時,公式可以簡化成:

其中n是樣本容量,N是總體容量,σ是總體標(biāo)準(zhǔn)差,σ(x拔)是樣本標(biāo)準(zhǔn)差。
重點來了:
①如果總體服從正態(tài)分布時:任何樣本容量下的(x拔)的抽樣分布都是正態(tài)分布。
②總體不服從正態(tài)分布時:
a.中心極限定理:從總體中抽取容量為n的簡單隨機樣本,當(dāng)樣本的容量額很大時,樣本均值(x拔)的抽樣分布近似服從正態(tài)概率分布。
b.其實在大多數(shù)的應(yīng)用中,樣本容量大于30時,(x拔)的抽樣分布近似服 從正態(tài)概率分布。
(2)樣本比率的抽樣分布
(p拔)的抽樣:樣本比率(p拔)的所有可能值的概率分布。
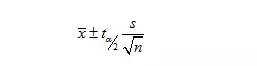
其中:x=具有感興趣特征的個體的個數(shù),n=樣本容量。
(p拔)的數(shù)學(xué)期望:
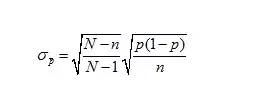
其中,p=總體比率。
(p拔)的標(biāo)準(zhǔn)差:
當(dāng)樣本容量占總體5%以上時,有求樣本標(biāo)準(zhǔn)差公式如下:
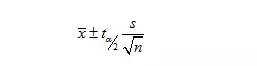
當(dāng)樣本容量占總體5%以下時,公式可以簡化成:

其中n是樣本容量,N是總體容量,p是總體比率,σ(p拔)是樣本標(biāo)準(zhǔn)差。
(p拔)的抽樣分布形態(tài):

在上面的公式之中,x是一個服從二項分布的隨機變量,n為常數(shù),所以(p拔)也是離散型的概率分布。其實,如果樣本容量足夠大,并且np>=5和n(1-p)>=5,二項分布可用正態(tài)分布近似,(p拔)的抽樣分布可用正態(tài)分布來近似。
四. 區(qū)間估計
點估計是用于估計總體參數(shù)的樣本統(tǒng)計量,但是我們不可能通過點估計就給出總體參數(shù)的一個精確值,更穩(wěn)妥的方法是加減一個邊際誤差,通過一個區(qū)間值來估計(區(qū)間估計)。
1. 總體均值的區(qū)間的估計
(1)總體均值的區(qū)間的估計:σ已知情形。
對總體均值進行估計時:
①要利用總體標(biāo)準(zhǔn)差σ計算邊際誤差。
②抽樣前可通過大量歷史數(shù)據(jù)估計總體標(biāo)準(zhǔn)差。
下面做一道例題感受下吧:
這是一道有關(guān)顧客購物消費額的問題,根據(jù)歷史數(shù)據(jù),σ=20美元,并且總體服正態(tài)分布。現(xiàn)在抽取n=100名顧客的簡單隨機樣本,其樣本均值(x拔)=82美元。求總體均值的區(qū)間估計。
開始解答了:
①總體服從正態(tài)分布,所以樣本均值的抽樣分布也是正態(tài)分布。
②根據(jù)σ=20美元,得出:

③所以x拔的抽樣分布服從標(biāo)準(zhǔn)差為σ(x拔)=2的正態(tài)分布。
④任何正態(tài)分布的隨機變量都有95%的值在均值附近加減1.96個標(biāo)準(zhǔn)差以內(nèi)(通過查表可得)。
⑤σ(x拔)=2,(x拔)所有值的95%都落在【u加減1.96σ(x拔)也即是u加減3.92】。
也即是:

(x拔)=82美元


所以u的區(qū)間估計是(78.08,85.92)。
其中這個區(qū)間是在95%置信水平下建立的,置信系數(shù)為0.05。區(qū)間(78.08,85.92)為95%的置信區(qū)間。
根據(jù)公式來計算區(qū)間,邊際誤差、區(qū)間估計如下圖所示:

所以:

在90%,95%,99%的置信水平情況下:

所以90%,99%的置信水平下的置信區(qū)間為:

其實我們也能得出這樣的結(jié)論:想要達到的置信水平越高,邊際誤差就要越大,置信區(qū)間也是越寬。
(2)總體均值的區(qū)間估計:σ未知情形。
①當(dāng)σ未知時,我們需要利用同一個樣本估計u和σ兩個參數(shù)。
②用s估計σ時,邊際誤差和總體均值的區(qū)間估計依據(jù)t分布。
并且總體是不是正態(tài)分布用t分布來估計效果都是挺好的。
t分布
有一類相似的概率分布組成的分布族;某個特定的t分布依賴于自由度的參數(shù);自由度越大,t分布與標(biāo)準(zhǔn)正態(tài)分布的差別越小;t分布的均值為0。
其中與z分布有類似的情況的是:

例如:
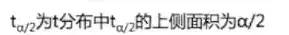
利用的計算公式如下:
邊際誤差:

區(qū)間估計:

樣本標(biāo)準(zhǔn)差:
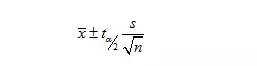
自由度:n-1。
注:

(3)樣本容量的確定
我們可以選擇足夠的樣本容量以達到所希望的邊際誤差。
由于邊際誤差公式為:

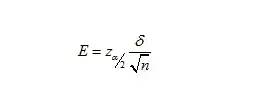
所以總體均值區(qū)間估計中的樣本容量為:

注:

如果σ未知,可通過以下方法確定σ的初始值。
①根據(jù)以前研究中的數(shù)據(jù)計算總體標(biāo)準(zhǔn)差的估計值。
②利用實驗性研究,選取一個初始樣本,以初始樣本的標(biāo)準(zhǔn)差做估計值。
③對σ進行判斷或最優(yōu)猜測:計算極差/4為標(biāo)準(zhǔn)差的粗略估計。
由于和總體均值的區(qū)間估計類似,這里就不詳細說明了,直接上公式:
邊際誤差:

區(qū)間估計:

(1)樣本容量的確定
我們可以選擇足夠的樣本容量以達到所希望的邊際誤差。
邊際誤差:

所以樣本容量為:
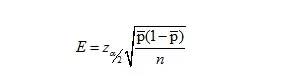
由于抽樣前(p拔)是未知的,不能用于計算達到預(yù)期的邊際誤差所要的樣本容量,因此令(p星)表示(p拔)的計劃值:

p星的確定
①用以前研究中類似的樣本的樣本比率作為計劃值。
②利用實驗性的研究,選取一個初始樣本,以初始樣本的樣本比例作為計劃值。
③使用判斷或最優(yōu)猜測作為計劃值。
④如果上述均不可,計劃值取為0.5,這是因為p(星)=0.5時,p星*(1-p星)取得最大值,同時樣本容量也能取的最大值。
5
五. 假設(shè)檢驗
何為假設(shè)檢驗?假設(shè)檢驗是對總體參數(shù)做一個嘗試性的假設(shè),該嘗試性的假設(shè)稱為原假設(shè),然后定義一個和原假設(shè)完全對立的假設(shè)叫做備選假設(shè)。其中備選假設(shè)是我們希望成立的論斷,原假設(shè)是我們不希望成立的論斷。
假設(shè)檢驗涉及討論的內(nèi)容有:
①總體均值的檢驗:σ已知和σ未知情形。
②總體比率的假設(shè)檢驗:σ已知和σ未知道。
但是下面主要討論在σ已知情形下,總體均值的檢驗,其他的根據(jù)區(qū)間估計中的證明和下面的例題都能很方便的理解出來。
σ已知情形
準(zhǔn)備一道例題,通過例子說明思路。
質(zhì)檢機構(gòu)檢查某品牌咖啡的標(biāo)簽上顯示裝有3磅咖啡,現(xiàn)在質(zhì)檢機構(gòu)需要確定每罐咖啡的質(zhì)量至少有三磅,以保證消費者權(quán)益。已知道σ=0.18,現(xiàn)在取得n=36罐咖啡組成一個隨機樣本,計算出(x拔)=2.92。
開始解答了:
①首先我們明白想要的結(jié)果是證明u<3,所以就提出了原假設(shè)和備選假設(shè)如下:h0:u>=3;Ha:u<3。
②其中我們在檢驗的過程允許以1%的可能性犯錯誤也即是 α=0.01。
③由于樣本n=36,σ=0.18,所本均值的抽樣分布是服從正態(tài)概率分布。

④所以當(dāng)(x拔)=2.92時,z=-2.67。
⑤因為原假設(shè)u是大于等于3的,所以我們就觀察z小于或等于-2.69的值,讓p值等于檢驗統(tǒng)計值z小于或等于-2.69的概率;利用標(biāo)準(zhǔn)正態(tài)概率表,z=-2.69時,p值=0.0038。
其中我們可以這樣理解z小于或者等于-2.69的概率p=0.0038這一事件的發(fā)生概率是非常的小,又加上允許犯錯的概率是0.01(也即是發(fā)生的概率是0.01結(jié)果是非常小的,我直接忽略了)。
所以我們直接認為z小于或者等于-2.69這一事件太小以至于我們認為他是不發(fā)生的。所以我們拒絕了H0:u>=3這一假設(shè)。所以,在0.01的顯著水平下有足夠的統(tǒng)計證據(jù)拒絕H0。











